Keystone High School Physics
1st Quarter - Week 2

Displacement
| The displacement of an object is defined as the vector distance from some initial point to a final point. It is therefore distinctly different from the distance traveled except in the case of straight line motion. The distance traveled divided by the time is called the speed, while the displacement divided by the time defines the average velocity. | |
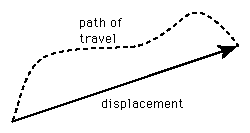 |
If the positions of the initial and final points are known, then the distance relationship can be used to find the displacement. |
| Δx = xf - xi | |
|---|---|
| displacement = change in position = final position - initial position | |
Velocity
Velocity is a vector quantity which refers to "the rate at which an object changes its position." Imagine a person moving rapidly - one step forward and one step back - always returning to the original starting position. While this might result in a frenzy of activity, it would result in a zero velocity. Because the person always returns to the original position, the motion would never result in a change in position. Since velocity is defined as the rate at which the position changes, this motion results in zero velocity. If a person in motion wishes to maximize their velocity, then that person must make every effort to maximize the amount that they are displaced from their original position. Every step must go into moving that person further from where he or she started. For certain, the person should never change directions and begin to return to the starting position. |
| vavg | = | Δx | = | xf - xi |
|---|---|---|---|---|
| Δt | tf - ti |
The correct unit for displacement is meters,m and the unit for time is seconds, s. |
| average velocity | = | change in position | = | displacement |
|---|---|---|---|---|
| change in time | time interval |
| Example: During a race on level ground, Casey covers 825 m in 137 s while running due west. Find Casey's average velocity. | |||||
|---|---|---|---|---|---|
| Because we are know both the displacement and the time we can use the average velocity equation. | |||||
| vavg | = | Δx | = | 825 m | = 6.02 m/s west |
| Δt | 137 s | ||||
Acceleration
Acceleration is a form of motion where the object�s velocity changes. It is most commonly measured in m/s/s. The formal definition for acceleration would be the rate of change of velocity with respect to time. Stand by the last locker in a row. with your first step walk the distance of one locker. With your next step walk the distance of 2 lockers. Then, 3, 4, so on and so forth. What you are experiencing is an acceleration of one locker per step per step. This means that with each step you increase your rate by one locker per step. |
| aavg | = | Δv | = | vf - vi |
|---|---|---|---|---|
| Δt | tf - ti |
The correct unit for velocity is meters per second,m/s and the unit for time is seconds, s. Therefore the unit for acceleration is meters per second per second,m/s/s or m/s2. |
| average acceleration | = | change in velocity |
|---|---|---|
| change in time |
| Example: As a bus comes to a normal stop, it slows from 9.00 m/s to 0.00 m/s in 5.00 s. Find the average acceleration of the bus. | |||||
|---|---|---|---|---|---|
| Because we are know both the initial and final velocities along with the time we can use the average acceleration equation. | |||||
| vavg | = | Δx | = | 0.00 m/s - 9.00 m/s | = -1.80 m/s2 |
| Δt | 5.00 s | ||||
Constant Acceleration
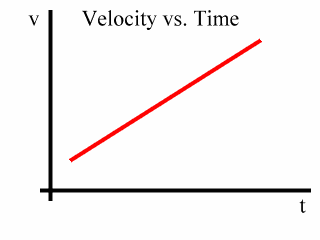
First, let's consider the following velocity vs. time graph which shows a constant acceleration: Since the slope of this graph is the acceleration, and since the slope of this graph is constant, the acceleration represented here is constant. Also, remember that the area under this graph is the displacement, or change in position, of the object. Now, let's consider a time period over which this acceleration occurs. We will concern ourselves with a time period from t1to t2: At t1 we will say that the velocity is v1. And at t2 we will say that the velocity is v2: Now, recall that the area under this graph is the displacement of the object. So the area under the graph from t1 to t2 represents the displacement of the object over the time period from t1 to t2. Notice that this area is a trapezoid, here shaded blue: In general, the area of a trapezoid equals one-half times the sum of the bases times the height. This trapezoid, one might say, is "on its side" since the bases are vertical and the height is horizontal. Now, back to our v vs. t graph. Notice that Base 1 is v1, Base 2 is v2, and that the Height is the time period from t1 to t2. The formula for the area of the trapezoid is: We will call the time period from t1 to t2 to be simply t. That is:
So, the height of the trapezoid is t, and the two bases are v1 and v2. Therefore, the area of the trapezoid is:
Now, we remember that the area of a v vs. t graph is the change in position, or the displacement, and that displacement is symbolized with Δx. Therefore, this:
Becomes:
Now, as far as the acceleration over the time period t is concerned, v1 is the velocity at the start of the acceleration. That is, v1 is the first or original velocity; so, the symbol v1 and the symbol vi mean the same thing; that is:
And v2 is the velocity at the end of the acceleration. That is, v2 is the final velocity, and the symbols v2 and vf mean the same thing; that is:
So, this:
Is the same as:
|
| Example: A racing car reaches a speed of 42 m/s. It then begins a uniform negative acceleration, using its parachute and braking system, and comes to a rest 5.5 s later. Find how far the car moves while stopping. | |||||
|---|---|---|---|---|---|
| Because we are know both the initial (42 m/s) and final velocities (0 m/s) along with the time (5.5s) we can use the displacement with constant acceleration equation. | |||||
| Δx= ½(vi + vf)t | |||||
| Δx= ½(42 m/s + 0 m/s)(5.5 s) | |||||
| Δx= ½(42 m/s)(5.5 s) | |||||
| Δx= (21 m/s)(5.5 s) | |||||
| Δx= 120 m | |||||