| Return to First Quarter Page
Net Forces in Action
| In my opinion this is the hardest section of the first semester. The reason for this is because of what you are used to in problem solving. For years you have been given one equation and then a group of values to plug into that equation and solve. Earlier this quarter we were given a series of equations and a set of variables and you had to figure out which equation to use. This material takes it even a step further. Given the information from the problem you will be asked to generate the equation and then solve for the unknown. |
| |
| The best way to understand this is to jump in with both feet and try a few examples. So here we go. |
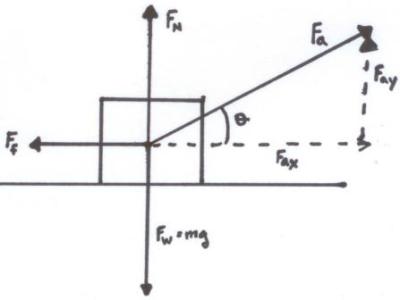
| EXAMPLE: A student moves a box of books by attaching a rope to the box and pulling with a force of 90.0 N at an angle of 30.0°, as shown in the figure below. The box of books has a mass of 20.0 kg, and the coefficient of kinetic friction between the bottom of the box and the sidewalk is .50. Find the acceleration of the box. |
 |
| |
| Ultimately we are solving for FNet = ma. The difficulty is solving for the FNet. In order to solve this problem we are going to have to draw a free body diagram as shown above. From this diagram we will generate two equations, one for the x-direction, ΣFx and one for the y-direction, ΣFy
|
| |
| First, we know the sum in the y direction is 0 becuase the box is not falling through the floor or flying through the air,so for the y direction we will add all of the forces in the positive y direction and subtract all of the forces in the negative y direction to get: |
| |
| ΣFy = FN + Fa,y - Fw = 0 |
| |
| Rearranging the formula to solve for FN yields: |
| |
| FN = Fw - Fa,y |
| |
| We can then solve for FN |
| |
| FN = mg - Fa(sin θ) |
| |
| FN = (20.0 kg)(9.81 m/s2) - 90.0 N(sin 30.0°) |
| |
| FN = 196 N - 45 N = 151 N |
| |
| The next step is to form an equation for all of the forces in the x direction |
| |
| ΣFx = Fa,x - Ff = ma |
| |
| We can now make some substitutions for our forces. |
| |
| Fa(cos θ) - μFN = ma |
| |
| (90.0 N)(cos 30.0) - (.50)(151 N) = ma |
| |
| 77.9 N - 75.5 N = 2.4 N = (20.0 kg)a |
| |
| Dividing both sides by the 20.0 kg we solve for a. |
| |
| a = .12 m/s2 |
| Now on to our second example. |
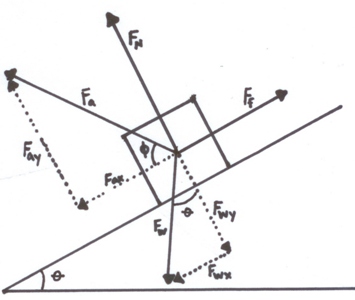
| EXAMPLE: A student moves a crate of plaster statues down the hall of a museum by pulling on a rope attached to the box. When the student reaches the 12.0° downward handicapped ramp he begins to accelerate downward. The student pulls with a force of 1850 N at an angle of 25.0° above the floor. The box has a mass of 350 kg and the μ between the box and the floor is .27. Find the acceleration of the box.
|
 |
| |
| Once again, we are ultimately solving for FNet = ma. The difficulty is solving for the FNet. In order to solve this problem we are going to have to draw a free body diagram as shown above. From this diagram we will generate two equations, one for the x-direction, ΣFx and one for the y-direction, ΣFy
|
| |
| First, we know the sum in the y direction is 0 becuase the box is not falling through the floor or flying through the air,so for the y direction we will add all of the forces in the positive y direction and subtract all of the forces in the negative y direction to get: |
| |
| ΣFy = FN + Fa,y - Fw,y = 0 |
| |
| Rearranging the formula to solve for FN yields: |
| |
| FN = Fw,y - Fa,y |
| |
| We can then solve for FN |
| |
| FN = mg(cos θ) - Fa(sin φ) |
| |
| FN = (350 kg)(9.81 m/s2)(cos 12.0°) - 1850 N(sin 25.0°) |
| |
| FN = 3358.5 N - 781.8 N = 2576.7 N |
| |
| The next step is to form an equation for all of the forces in the x direction |
| |
| ΣFx = Fa,x + Fw,x - Ff = ma |
| |
| We can now make some substitutions for our forces. |
| |
| Fa(cos φ) + mg(sin θ) - μFN = ma |
| |
| (1850 N)(cos 25.0°) + (350 kg)(9.81 m/s2)(sin 12.0°) - (.27)(2576.7 N) = ma |
| |
| 1676.7 + 713.9 - 695.7 = ma |
| |
| 1694.9 = (350 kg)a |
| |
| a = 4.84 m/s2 |
Go To Next Lesson
Return to First Quarter Page
|



