| Return to First Quarter Page
Mechanical Energy and Power
| CONSERVATION OF MECHANICAL ENERGY |
| Mechanical energy is the energy which is possessed by an object due to its motion or due to its position. Mechanical energy can be either kinetic energy (energy of motion) or potential energy (stored energy of position). Objects have mechanical energy if they are in motion and/or if they are at some position relative to a zero potential energy position (for example, a brick held at a vertical position above the ground or zero height position). A moving car possesses mechanical energy due to its motion (kinetic energy). A moving baseball possesses mechanical energy due to both its high speed (kinetic energy) and its vertical position above the ground (gravitational potential energy). A World Civilization book at rest on the top shelf of a locker possesses mechanical energy due to its vertical position above the ground (gravitational potential energy). A barbell lifted high above a weightlifter's head possesses mechanical energy due to its vertical position above the ground (gravitational potential energy). A drawn bow possesses mechanical energy due to its stretched position (elastic potential energy). |
| |
| Numerous examples can be given of how an object with mechanical energy can harness that energy in order to apply a force to cause another object to be displaced. A classic example involves the massive wrecking ball of a demolition machine. The wrecking ball is a massive object which is swung backwards to a high position and allowed to swing forward into building structure or other object in order to demolish it. Upon hitting the structure, the wrecking ball applies a force to it in order to cause the wall of the structure to be displaced. The diagram below depicts the process by which the mechanical energy of a wrecking ball can be used to do work. |
| |
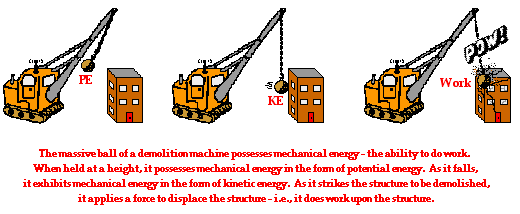 |
| |
| As already mentioned, the mechanical energy of an object can be the result of its motion (i.e., kinetic energy) and/or the result of its stored energy of position (i.e., potential energy). The total amount of mechanical energy is merely the sum of the potential energy and the kinetic energy. This sum is simply referred to as the total mechanical energy, ME. |
| |
| The formula used for the conservation of mechanical energy is: |
| This means that the total amount of mechanical energy at the start of an interaction is equal to the amount of mechanical energy at the end. We can also substitute the values of potential and kinetic energy into this formula. |
| Let's take a look at an example of this type of problem. |
| EXAMPLE: Starting from rest, a 25.0 kg child zooms down a frictionless slide with an initial height of 3.00 m. What is her speed at the bottom of the slide?
|
| |
| We are going to start out with our conservation of mechanical energy equation and we can make a few observations. |
| |
| ½mvi2 + mghi = ½mvf2 + mghf |
| |
| The first observation that we will make is that she is starting at rest and with an initial velocity of zero we also have an initial kinetic energy of zero. Also we end up on the ground at the end of the slide so we have a height of zero. If your height is zero then your potential energy is zero. |
| |
| ½mvi2 = 0 and mghf = 0 |
| |
| Rewriting what is left leaves us with: |
| mghi = ½mvf2 |
| |
| We can now rearrange this equation to solve for vf noting that the mass of the child will not change as the move down the slide so it can be cancelled out. |
| vf = √(2ghi) = √(2(9.81 m/s2)(3.00 m)) = 7.67 m/s |
| WORK - KINETIC ENERGY THEOREM |
| The relationship between work and kinetic energy is a relative easy one with both of them being measured in Joules. The point of the theorem is that mechanical energy is not conserved, especially when friction is involved. The work that is done by friction is equal to the change in mechanical energy. Therefore energy can be lost in either kinetic or potential energy. For the sake of simplicity we will look at it from the perspective of kinetic energy. The formula for the relationship is: |
| EXAMPLE: On a frozen pond, a person kicks a 10.0 kg sled, giving it an initial speed of 2.2 m/s. How far does the sled move if the coefficient of kinetic friction between the sled and the ice is .10? |
| |
| To solve this problem we will need both the definition of work and the work-kinetic energy theorem. |
| |
| Wnet = Fd(cosθ) and Wnet = ΔKE |
| |
| Rewriting this we get: |
| |
| Fd(cosθ) = ΔKE = KEf - KEi
|
| |
| There are a few substitutions that can be made as we come to a stop so the KEf = 0 and the net force acting on the sled is friction which is μFN or μmg. Substituting these values gives us: |
| μmgd(cosθ) = ½mvi2
|
| |
| We can cancel out the masses and we are solving for how far the sled travels so we need to rearrange the equation to solve for d. |
| d = |
vi2 |
= |
(2.2 m/s)2 |
= -24 J |
|
|
| μg(cosθ) |
(.10)(9.81 m/s2)(cos 180°)
|
| POWER |
| The quantity work has to do with a force causing a displacement. Work has nothing to do with the amount of time that this force acts to cause the displacement. Sometimes, the work is done very quickly and other times the work is done rather slowly. For example, a rock climber takes an abnormally long time to elevate her body up a few meters along the side of a cliff. On the other hand, a trail hiker (who selects the easier path up the mountain) might elevate her body a few meters in a short amount of time. The two people might do the same amount of work, yet the hiker does the work in considerably less time than the rock climber. The quantity which has to do with the rate at which a certain amount of work is done is known as the power. The hiker has a greater power rating than the rock climber. |
| |
| Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation. |
| Since we know that work is equal to force times distance we can rewrite the equation so that it is force times (distance divided by time). This new form allows us to substitute velocity for distance divided by time leaving the alternative form of the power equation: |
| The standard metric unit of power is the Watt. As is implied by the equation for power, a unit of power is equivalent to a unit of work divided by a unit of time. Thus, a Watt is equivalent to a Joule/second. For historical reasons, the horsepower is occasionally used to describe the power delivered by a machine. One horsepower is equivalent to approximately 750 Watts. |
| |
| And, finally our example for power. |
| EXAMPLE: A 193 kg curtain needs to be raised 7.5 m in as close to 5.0 s as possible. How much power is needed by the motor to lift the curtain? |
| We will use the power equation and substitute Fd in for work and then mg for the force to solve for power. |
| P = |
W |
= |
Fd |
= |
mgd |
= |
(193 kg)(9.81 m/s2)(7.5 m) |
|
|
|
|
| Δt |
Δt |
Δt |
5.0 s |
| P = 2.8 x 103 W = 2.8 kW |
Go To Next Lesson
Return to First Quarter Page
|


