Keystone High School Physics
1st Quarter - Week 4

Vectors

In order to understand the discoveries of Newton, we must have an understanding of three basic quantities: (1) velocity, (2) acceleration, and (3) force. In this section we define the first two, and in the next we shall introduce forces. These three quantities have a common feature: they are what mathematicians call vectors.

Examples of Scalar Quantities

Vectors are quantities that require not only a magnitude, but a direction to specify them completely. Let us illustrate by first citing some examples of quantities that are not vectors. The number of gallons of gasoline in the fuel tank of your car is an example of a quantitity that can be specified by a single number---it makes no sense to talk about a "direction" associated with the amount of gasoline in a tank. Such quantities, which can be specified by giving a single number (in appropriate units), are called scalars. Other examples of scalar quantities include the temperature, your weight, or the population of a country; these are scalars because they are completely defined by a single number (with appropriate units).

Examples of Vector Quantities

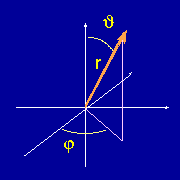However, consider a velocity. If we say that a car is going 70 km/hour, we have not completely specified its motion, because we have not specified the direction that it is going. Thus, velocity is an example of a vector quantity. A vector generally requires more than one number to specify it; in this example we could give the magnitude of the velocity (70km/hour), a compass heading to specify the direction (say 30 degrees from North), and an number giving the vertical angle with respect to the Earth's surface (zero degrees except in chase scenes from action movies!). The adjacent figure shows a typical coordinate system for specifying a vector in terms of a length r and two angles, theta and phi.

Graphical Representation of Vectors

Vectors are often distinguished from scalar quantities either by placing a small arrow over the quantity, or by writing the quantitity in a bold font. It is also common to indicate a vector by drawing an arrow whose length is proportional to the magnitude of the vector, and whose direction specifies the orientation of the vector.

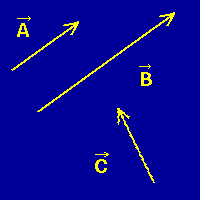
In the adjacent image we show graphical representations for three vectors. Vectors A and C have the same magnitude but different directions. Vector B has the same orientation as vector A, but has a magnitude that is twice as large. Each of these represents a different vector, because for two vectors to be equivalent they must have both the same magnitudes and the same orientations.

Pythagorean Theorem

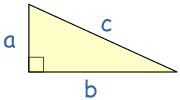
Using what we have learned in previous math classes we can solve for simple vectors using the Pythagorean Theorem. The square of a (a²) plus the square of b (b²) is equal to the square of c (c²):

a² + b² = c²

EXAMPLE: What is the diagonal distance across a square with all sides at the unit of 1?

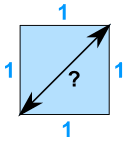a² + b² = c²

1² + 1² = c²

1 + 1 = c²

2 = c²

c² = 2

c = √2 = 1.4142...

Right Triangles

Sine, Cosine and Tangent are all based on a Right-Angled Triangle

Before getting stuck into the functions, it helps to give a name to each side of a right triangle: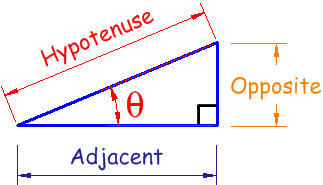

triangle showing Opposite, Adjacent and Hypotenuse

"Opposite" is opposite to the angle θ
"Adjacent" is adjacent (next to) to the angle θ
"Hypotenuse" is the long one

Adjacent is always next to the angle (and opposite is opposite the angle):

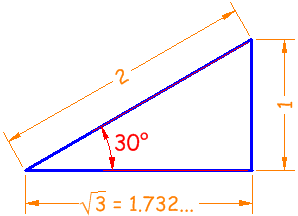
Example 1: What are the sine, cosine and tangent of a 30° triangle?

The classic 30° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of √(3):

Now we know the lengths, we can calculate the functions:

Sine	sin(30°) = 1 / 2 = 0.5
Cosine	cos(30°) = 1.732 / 2 = 0.866
Tangent	tan(30°) = 1 / 1.732 = 0.577

Go To Next Lesson

Return to First Quarter Page

Email: [email protected]

Phone: (440) 355-5132 ext. 1163