| Return to First Quarter Page
Projectile Motion
| A projectile is an object upon which the only force acting is gravity. There are a variety of examples of projectiles. An object dropped from rest is a projectile (provided that the influence of air resistance is negligible). An object which is thrown vertically upward is also a projectile (provided that the influence of air resistance is negligible). And an object is which thrown upward at an angle to the horizontal is also a projectile (provided that the influence of air resistance is negligible). A projectile is any object which once projected or dropped continues in motion by its own inertia and is influenced only by the downward force of gravity. |
 |
| By definition, a projectile has only one force acting upon it - the force of gravity. If there was any other force acting upon an object, then that object would not be a projectile. Thus, the free-body diagram of a projectile would show a single force acting downwards and labeled force of gravity (or simply Fgrav). Regardless of whether a projectile is moving downwards, upwards, upwards and rightwards, or downwards and leftwards, the free-body diagram of the projectile is still as depicted in the diagram at the right. By definition, a projectile is any object upon which the only force is gravity. |
| If we neglect the force of gravity and launch an object horizontally we would find that it would travel in a straight path forever according to Newton's First Law of Motion. This is shown in the image on the left below. If gravity is turned on we see that the path is altered due to the new force acting on it. This is shown in the image on the right below.
|
 |
 |
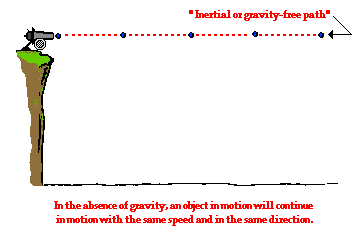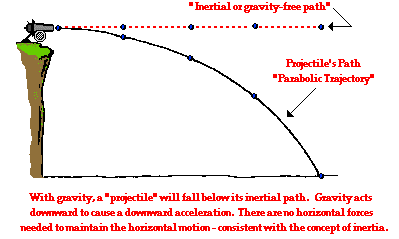| The formulas for projectile motion are similar to those we have discussed earlier. Horizontally they are easy since the velocity in the horizontal direction is considered to be constant, so... |
| The vertical direction also has formulas that we have seen in the past. The only difference being we can ignore the initial velocity componant because we are launched horizontally and the vertical componant of the velocity would be zero. |
| It is important to remember that the value of g is -9.8 m/s2 |
| Let's try a couple of examples.
|
| Example: A movie director is shooting a scene that involves a stunt man jumping from an airplane into a pool. If the plane is 10.0 m off the ground and the plane is traveling 22.5 m/s, how far in front of the pool must the man jump to land in the water? |
|
Looking at the information that is given in the problem we can make a chart of givens.
- Δx = ?
- Δy = -10.0 m
- vy,i = 0 m/s
- vx = 22.5 m/s
- g = -9.8 m/s2
- Δt = ?
From the data we see that we do not have a Δx and it is also important to realize that the only variable that works in both directions is time. So if we solve for time in the y direction we can then use it in the x direction. |
| Use this equation: Δy = ½g(Δt)2 to solve for Δt |
| 2Δy |
= |
Δt2 |
|
| g |
| √ ( |
2Δy
| ) = Δt |
|
| g |
| √ ( |
2(-10.0 m)
| ) = Δt |
|
| -9.8 m/s2 |
| 1.43 s = Δt |
| Now that we have time we can use this equation: Δx = vxΔt and solve for Δx |
| Δx = vxΔt |
| Δx = (22.5 m/s)(1.43 s) |
| Δx = 32.2 m |
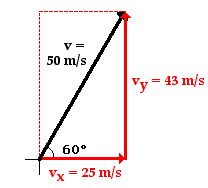 The preceding example is perfect if the projectile is launched horizontally. But, what happens if the object is launched at an angle. The biggest difference is in the initial velocities.
We must consider that if the velocity is at an angle then it is made of two componant velocities. In the previous lesson we discussed vectors and how, using sin and cos, we can break a resultant vector into one along the x-axis and the other along the y-axis. This can be seen in the figure to the right.
The following are the equations for the componants for the initial velocity vector: |
| vx,i = vicos θ and vy,i = vi sin θ |
| The following equations can be used to solve for PROJECTILES LAUNCHED AT AN ANGLE: |
| Let's try a classic example of projectile motion.
|
| Example: A zookeeper finds an escaped monkey sitting on a light pole. Aiming her tranquilizer gun at the monkey, the zookeeper kneels 10.0m from the light pole, which is 5.0m high. The tip of her gun is 1.0m above the ground. The monkey tries to trick the zookeeper by dropping a banana, and then continues to sit on the pole. At the moment the monkey releases the banana, the zookeeper shoots. If the tranquilizer dart travels at 50.0m/s, will the dart hit the monkey, the banana, or nothing? |
| |
| The first thing we are going to do is draw a diagram of what is happening using the given values. From the diagram below we can see that we are given both a height and a length. From those two values we can calculate the angle in which the zookeeper was shooting. |
 |
| θ = tan-1( |
Δy |
) = tan-1( |
4.00 m |
) = 21.8° |
|
|
| Δx |
10.0 m |
| Now that we have the value of the angle we can use the Δx equation to solve for how long the dart was in the air. This is important because time is the same no matter if you are moving horizontally or vertically. |
| Δx = vi(cos θ)Δt |
| |
| Rearranging for Δt we get: |
| |
| Δt = |
Δx |
= |
10.0 m |
= .215 s |
|
|
| vi(cos θ) |
(50.0 m/s)(cos 21.8°)
|
| We now know how long the dart is in the air. We already knew how far the monkey traveled, 0.0 m, because he did not move. What we can solve for, however, is how far the banana fell. We can do this by using the displacement in freefall equation from the previous lesson. |
| Δy = ½g(Δt)2 = ½(-9.81 m/s2)(.215 s)2 = -.227 m |
| We have just determined that the banana fell .227 m. So what we have to determine now is the position of the dart relative to the original position of the gun. This can be done using our newest Δy equation. |
| Δy = vi(sin θ)Δt + ½gΔt2 |
| Δy = (50.0 m/s)(sin 21.8°)(.215 s) + ½(-9.81m/s2)(.215 s)2 |
| Δy = 3.99 m - .227 m = 3.76 m |
| From the information we just attained we can see that the dart and the banana will end up in the same position and they will meet and the zookeeper will need to find another way to capture the monkey. |
Go To Next Lesson
Return to First Quarter Page
|
