| Return to First Quarter Page
Forces
| A force is a push or pull upon an object resulting from the object's interaction with another object. Whenever there is an interaction between two objects, there is a force upon each of the objects. When the interaction ceases, the two objects no longer experience the force. Forces only exist as a result of an interaction. |
| |
| Force is a quantity which is measured using the standard metric unit known as the Newton. A Newton is abbreviated by a "N." To say "10.0 N" means 10.0 Newtons of force. One Newton is the amount of force required to give a 1-kg mass an acceleration of 1 m/s/s. Thus, the following unit equivalency can be stated: |
| |
| 1 Newton = 1 kg m/s2 |
| |
| A force is a vector quantity. As learned in an earlier unit, a vector quantity is a quantity which has both magnitude and direction. To fully describe the force acting upon an object, you must describe both the magnitude (size or numerical value) and the direction. Thus, 10 Newtons is not a full description of the force acting upon an object. In contrast, 10 Newtons, downwards is a complete description of the force acting upon an object; both the magnitude (10 Newtons) and the direction (downwards) are given. |
| |
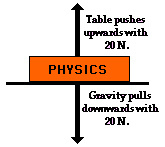 Because a force is a vector which has a direction, it is common to represent forces using diagrams in which a force is represented by an arrow. Such vector diagrams were introduced in an earlier unit and are used throughout the of physics. The size of the arrow is reflective of the magnitude of the force and the direction of the arrow reveals the direction which the force is acting. (Such diagrams are known as free-body diagrams and are discussed later in this lesson.) Furthermore, because forces are vectors, the affect of an individual force upon an object is often canceled by the affect of another force. For example, the affect of a 20-Newton upward force acting upon a book is canceled by the affect of a 20-Newton downward force acting upon the book. In such instances, it is said that the two individual forces balance each other; there would be no unbalanced force acting upon the book. Because a force is a vector which has a direction, it is common to represent forces using diagrams in which a force is represented by an arrow. Such vector diagrams were introduced in an earlier unit and are used throughout the of physics. The size of the arrow is reflective of the magnitude of the force and the direction of the arrow reveals the direction which the force is acting. (Such diagrams are known as free-body diagrams and are discussed later in this lesson.) Furthermore, because forces are vectors, the affect of an individual force upon an object is often canceled by the affect of another force. For example, the affect of a 20-Newton upward force acting upon a book is canceled by the affect of a 20-Newton downward force acting upon the book. In such instances, it is said that the two individual forces balance each other; there would be no unbalanced force acting upon the book. |
| |
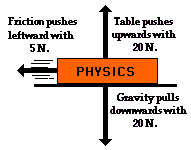 Other situations could be imagined in which two of the individual vector forces cancel each other ("balance"), yet a third individual force exists that is not balanced by another force. For example, imagine a book sliding across the rough surface of a table from left to right. The downward force of gravity and the upward force of the table supporting the book act in opposite directions and thus balance each other. However, the force of friction acts leftwards, and there is no rightward force to balance it. In this case, an unbalanced force acts upon the book to change its state of motion. Other situations could be imagined in which two of the individual vector forces cancel each other ("balance"), yet a third individual force exists that is not balanced by another force. For example, imagine a book sliding across the rough surface of a table from left to right. The downward force of gravity and the upward force of the table supporting the book act in opposite directions and thus balance each other. However, the force of friction acts leftwards, and there is no rightward force to balance it. In this case, an unbalanced force acts upon the book to change its state of motion. |
| |
| Newton's First Law of Motion states that an object at rest will remain at rest, and an object in motion will remain in constant linear motion unless it experiences a net external force. This net external force can be determined through the use of a free body diagram. |
| |
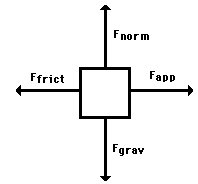 Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams which were discussed in an earlier unit. These diagrams will be used throughout our study of physics. The size of the arrow in a free-body diagram is reflects the magnitude of the force. The direction of the arrow shows the direction which the force is acting. Each force arrow in the diagram is labeled to indicate the exact type of force. It is generally customary in a free-body diagram to represent the object by a box and to draw the force arrow from the center of the box outward in the direction which the force is acting. An example of a free-body diagram is shown at the right. Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams which were discussed in an earlier unit. These diagrams will be used throughout our study of physics. The size of the arrow in a free-body diagram is reflects the magnitude of the force. The direction of the arrow shows the direction which the force is acting. Each force arrow in the diagram is labeled to indicate the exact type of force. It is generally customary in a free-body diagram to represent the object by a box and to draw the force arrow from the center of the box outward in the direction which the force is acting. An example of a free-body diagram is shown at the right. |
| |
| The free-body diagram above depicts four forces acting upon the object. Objects do not necessarily always have four forces acting upon them. There will be cases in which the number of forces depicted by a free-body diagram will be one, two, or three. There is no hard and fast rule about the number of forces which must be drawn in a free-body diagram. The only rule for drawing free-body diagrams is to depict all the forces which exist for that object in the given situation. Thus, to construct free-body diagrams, it is extremely important to know the various types of forces. If given a description of a physical situation, begin by using your understanding of the force types to identify which forces are present. Then determine the direction in which each force is acting. Finally, draw a box and add arrows for each existing force in the appropriate direction; label each force arrow according to its type. |
| |
| Newton's Second Law of Motion states that the acceleration of an object is directly proportional to the net external force acting on the object and inversely proportional to the mass of the object. |
| |
| EXAMPLE: A 5.5 kg watermelon is pushed across a table. If the acceleration of the watermelon is 4.2 m/s2 to the right, find the net external force exerted on the watermelon. |
| |
| ΣF = ma |
| ΣF = (5.5 kg)(4.2 m/s2) |
| ΣF = 23 kg m/s2 |
| ΣF = 23 N, to the right |
| Newton's Third Law of Motion is that for every action there is an equal and opposite reaction. This creates something called action-reaction pairs. One action is after or in response to the first action. A hammer pounding a nail into wood. Or even stepping off of a boat that is not tied to the dock. |
| |
| There has always been confusion over the difference between mass and weight. The mass is a measure of how much matter is present and is the same regardless of location in the universe. Weight is actually the force due to the acceleration of gravity. Since all materials will fall at the same rate, g, we can change our force equation to apply to this special circumstance. For the force due to gravity we have F = mg, and weight is measured in Newtons. |
| |
| The force of friction is the force exerted by a surface as an object moves across it or makes an effort to move across it. Kinetic friction results when an object slides across a surface. As an example, consider pushing a box across a floor. The floor surface offers resistance to the movement of the box. We often say that the floor exerts a friction force upon the box. This is an example of a kinetic friction force since it results from the sliding motion of the box. If a car slams on its brakes and skids to a stop (without antilock brakes), there is a kinetic friction force exerted upon the car tires by the roadway surface. Kinetic friction can be found using the normal force. The normal force is the support force exerted upon an object which is in contact with another stable object. For example, if a book is resting upon a surface, then the surface is exerting an upward force upon the book in order to support the weight of the book. The other value is the coefficient of kinetic friction. A simple chart of these values can be found on page 144 of your textbook. |
| We also have static friction to deal with. This is the amount of friction that holds an abject in place before it starts moving. This is why you always need to give that extra umph to get something moving and a little less effort to keep it moving. The force of static friction is always greater than the force of kinetic friction. |
| EXAMPLE: A 24 kg crate initially at rest on a horizontal surface requires a 75 N horizontal force to set it in motion. Find the coefficient of static friction between the crate and the floor. |
| We need to use the equation for the coefficient of static friction. |
| Ff,s = μsFN |
| We need to rearrange the equation to solve for μs |
| μs = |
Ff,s |
= |
Ff,s |
= |
75 N |
= .32 |
|
|
|
| FN |
mg |
(24 kg)(9.81 m/s2) |
| Note that the answer does not have a unit because the coefficient of friction is a unitless quantity. |
Go To Next Lesson
Return to First Quarter Page
|


 Because a force is a vector which has a direction, it is common to represent forces using diagrams in which a force is represented by an arrow. Such vector diagrams were introduced in an earlier unit and are used throughout the of physics. The size of the arrow is reflective of the magnitude of the force and the direction of the arrow reveals the direction which the force is acting. (Such diagrams are known as free-body diagrams and are discussed later in this lesson.) Furthermore, because forces are vectors, the affect of an individual force upon an object is often canceled by the affect of another force. For example, the affect of a 20-Newton upward force acting upon a book is canceled by the affect of a 20-Newton downward force acting upon the book. In such instances, it is said that the two individual forces balance each other; there would be no unbalanced force acting upon the book.
Because a force is a vector which has a direction, it is common to represent forces using diagrams in which a force is represented by an arrow. Such vector diagrams were introduced in an earlier unit and are used throughout the of physics. The size of the arrow is reflective of the magnitude of the force and the direction of the arrow reveals the direction which the force is acting. (Such diagrams are known as free-body diagrams and are discussed later in this lesson.) Furthermore, because forces are vectors, the affect of an individual force upon an object is often canceled by the affect of another force. For example, the affect of a 20-Newton upward force acting upon a book is canceled by the affect of a 20-Newton downward force acting upon the book. In such instances, it is said that the two individual forces balance each other; there would be no unbalanced force acting upon the book. Other situations could be imagined in which two of the individual vector forces cancel each other ("balance"), yet a third individual force exists that is not balanced by another force. For example, imagine a book sliding across the rough surface of a table from left to right. The downward force of gravity and the upward force of the table supporting the book act in opposite directions and thus balance each other. However, the force of friction acts leftwards, and there is no rightward force to balance it. In this case, an unbalanced force acts upon the book to change its state of motion.
Other situations could be imagined in which two of the individual vector forces cancel each other ("balance"), yet a third individual force exists that is not balanced by another force. For example, imagine a book sliding across the rough surface of a table from left to right. The downward force of gravity and the upward force of the table supporting the book act in opposite directions and thus balance each other. However, the force of friction acts leftwards, and there is no rightward force to balance it. In this case, an unbalanced force acts upon the book to change its state of motion. Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams which were discussed in an earlier unit. These diagrams will be used throughout our study of physics. The size of the arrow in a free-body diagram is reflects the magnitude of the force. The direction of the arrow shows the direction which the force is acting. Each force arrow in the diagram is labeled to indicate the exact type of force. It is generally customary in a free-body diagram to represent the object by a box and to draw the force arrow from the center of the box outward in the direction which the force is acting. An example of a free-body diagram is shown at the right.
Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams which were discussed in an earlier unit. These diagrams will be used throughout our study of physics. The size of the arrow in a free-body diagram is reflects the magnitude of the force. The direction of the arrow shows the direction which the force is acting. Each force arrow in the diagram is labeled to indicate the exact type of force. It is generally customary in a free-body diagram to represent the object by a box and to draw the force arrow from the center of the box outward in the direction which the force is acting. An example of a free-body diagram is shown at the right.